
楕円と楕円の交点 その3
プログラム修正 2019/01/21
軸角無し、同じ楕円で水平と垂直移動の判定値修正
プログラム修正 2018/11/18
多倍長演算 同じ座標値がダブって表示されない様にしました。
通常演算時の桁落ち対策値の修正。
プログラム修正 2018/09/01
軸角を100/3°(33.33333--)から30°に戻しました、100/3°でも問題はありません。(通常精度演算、多倍長演算)
軸角30°にした場合は、楕円角度の0.001°以下を丸めるのを廃止しました。(通常精度演算時、多倍長演算は元々角度の丸め無し)
軸角変更なしの計算の選択が出来る様にし、因数分解できなかった場合の方程式解法を追加しました。(通常精度演算)
プログラム追加 2017/08/06
多倍長演算の確認
プログラム修正 2017/07/30
楕円比(長径と短径の比)の大きいほうの計算時の軸角を30°から100 / 3 °(33.33333--)に変更しました。
(楕円の軸角の0.001°以下を丸めているので、計算時、軸角の整数倍の角度の発生はなくなります。)
プログラム修正 2017/07/24
二次方程式の解法条件を変更しました。 a = 0, h = 0, b = 0 => abs(a) < 1E-12, abs(h) < 1E-12, abs(b) < 1E-12
(演算誤差でゼロに成らない事がある為です)
プログラム修正 2017/07/19
交点の値に等しい値がある場合、紛らわしいので、そのうちの一つだけを表示するようにしました。
プログラム修正 2017/07/10
楕円比(長径と短径の比)の大きいほうの軸角を30°に設定して計算するように修正しました。
楕円1の座標を原点(0,0)にするのは変更有りません。
この変更で接線となる場合の計算結果が安定して得られるようになったと思います。
4次方程式での計算でも、楕円比の大きいほうの軸角を30°にして計算結果の安定を図っています。
三次方程式の解法に Double Extended 判別用ルーチン追加しました。
プログラム修正 2017/07/06
軸角が等しい楕円の軸角方向への移動時の交点計算ルーチンのミス修正
楕円弧モード追加 2017/06/22
楕円弧の無い部分には交点の丸表示が出ないようにしました。
プログラム修正 2017/06/05
1 三次方程式の解法時 虚数部を誤差とする値の変更 1E-14 ->
1E-6 計算誤差は 7E-8 程度
計算誤差が思った以上に大きく、Extended で計算しても 1E-8 計算誤差は 5E-10 程度
2 最後の連立方程式で交点を求める計算の手順ミスの修正
ペンシルと因数分解による方法では、extended(10byte)でも計算精度が不足します、double(8byte)では、接線に近い場合大きくズレた値となる場合があります。
この方法の場合は、接点の精度として、小数点以下1桁より高い精度が必要な場合、多倍長演算が必須です。
軸角度を30°に変換しなければ、多少は桁落ちが少なくなると思い、軸角の変更をしないルーチンの追加をしてみましたが、軸角が微小角で交点が接線に近いとき大きな値のズレが発生するようです。
大きなズレの発生は、四次二次方程式による方法より、方程式の解法が多く、方程式の解法を行う度に、桁落ちより答えが出ないのを防ぐ為、微小な値の丸めを行っている為です。
double(8byte)の精度でも、それなりの値が出る様に色々試みましたが、無理なようなので、この辺(2019/01/21)で検討を打ち切る事にしました。
追加した軸角の変更をしない場合の計算
軸角の変更をしないと、正しい答えが出ない場合があります。
特に接線の計算は桁落ちの影響が大きくなり多倍長演算が必須のようです。
接線と交点の判別が難しく、この境目で大きな誤差がはっせいします。
あらためて再確認しました。
多倍長演算の確認
多倍長演算によるプログラムの確認をしました。
プログラムは、三次式への変換、三次方程式の解法、因数分解等の交点を計算する部分を多倍長演算に変更してみました。
double、Extended
での桁落ちによる問題がありましたが、本当に桁落ちの問題なのか確認をするためです。
計算時の軸角をゼロにすると、因数分解ができない条件があるのは変わりませんが、それ以外は、正しい結果が得られます。
double,
extendedでの値の誤差は、桁落ちによる問題であることが確認できました。
逆に桁落ちにより、丸めの効果が出ている場合があり、その場所に対しては、多倍長演算時は、誤差の修正の追加が必要です。
四次方程式で計算する場合は、軸対称となるとなる場合に解が得られない事がありましたが、因数分解による方法では、計算時の軸角をゼロにしないことと、桁落ちさえなければ問題なく答えが得られます。
しかし、四次方程式では、Doubleの精度でも、交点の結果に大きな誤差は発生しません。
二つの楕円の形状が等しい場合は、四次方程式の時と同じように、二次方程式の解法が必要なのを再確認しました。
多倍長演算
計算精度に Double
を使用すると、計算結果として 有効桁数7桁程度しか得ることが出来ません。
Extendedは x64
ではフォローしていませんので、高い精度を必用とする場合は多倍長演算を使用する必要があります。
そこで、多倍長演算の
MPArith
を使用したプログラムを作成しました。
多倍長演算ならば、有効桁数20桁以上の精度を得ることが出来ます。
多倍長演算は、楕円の交点を求める計算部分だけで、作図部分は不要なので使用していません。
FPUを使用していないので、演算時間は長くなります。
MPArithからmparith_2017-08-03.zipをダウンロードします。
ファイルの日付が変わるので、変わっていたら新しいのをダウンロードして下さい。
Zipファイルを解凍して、解凍したフォルダーにパス(ツール->オプション->Delphiオプション->ライブラリ->ライブラリパス)を追加し、Uses に mp_types, mp_realを追加すれば使用可能になります。
一般の四則演算(=+-*/)は使用できず全て専用のルーチンとなるのでプログラムが長くなります。
使用方法は、ホームページ及び、hlpファイルを見れば分かりますが、hlpファイルは古いタイプなので、Win10で見るためには、変換をするか、WinHlp32.exeを入れ替える必要があります。
解凍したホルダーの中に mp_intro.txt があるのでそれをメモ帳で開けばホームページの説明と同じものが表示されます。
ペンシル
楕円同士の交点の計算に、二次曲線同士の交点を安定して求める方法としてペンシルという方法があったので、プログラムを作成してみました。
楕円式の二元二次の係数を、3×3の行列式で表し、
det(C1-λC2)のdetの値がゼロになるようにすると、C1曲線と、2直線の交点になり容易に交点が求まるというものです。
λの値は、λを未知数として、C1-λC2の行列式をのdetの計算を行えば、三次方程式の aλ^3 + bλ^2 + cλ + d の各係数値を得ることが出来ます。
次に、三次方程式を解法すれば、容易にλの値を得ることが出来ます。
λの値は、実数解が三個、又は、実数解一個と複素数解二個となる場合があります。
λの値が、実数解となっても、因数分解値 (α1x + β1y + γ1)(α2x + β2y + γ2)に出来ない場合が沢山発生します。
λの値を、det(C1-λC2)に入れて、行列式を計算すると、ax^2 + 2hxy + by^2 + 2gx + 2fy + c の各係数を得ることができ、detの値がゼロであれば、これを(α1x + β1y + γ1)(α2x + β2y + γ2)の形に因数分解出来ると言う事ですが、実際には、二元二次にならずに、一元二次、一次方程式、或いは、y = c' 、x = c' の様な解に成ることがあります。
特に片方の軸角がゼロになる様に座標変換をしてしまうと、因数分解できない条件が沢山発生します。
筆算の場合は良いのかもしれませんが、プログラムを組む場合は問題です。
因数分解が出来た時は、一次式となるので、一次式としての連立方程式を解いても良いのですが、組み合わせが出来るので、二元二次の楕円の式に代入して、連立方程式を解いた方が問題が無いようです。
しかし、因数分解できない場合は、各係数の値によって、判別をして、それぞれの連立を方程式を解く必要があります。
問題は、計算による、桁落ちの問題です、λの値を入れて、差分の計算をするので、doubleで有効桁数15桁程度の場合、何桁目くらいを迄を正しい値とするかの問題が生じます。
三次方程式の解法にも当然桁落ちが発生するので、桁落ちの問題は、深刻です。
本来は、ゼロに成るはずが、ゼロに成らず、ゼロでないはずがゼロに成ってしまう問題です。
四次方程式を利用した場合も、同じ問題が出て、この場合は、二次方程式で解くか、四次方程式で解くかなので、判別が簡単でしたが、因数分解の場合は、条件が多くなり、複雑になります。
二つの楕円の大きさに大きな差があると、桁落ちの為、答えが出ません。
行列式の係数の値に応じて、計算の方法設定をします、最初に二元二次方程式の因数分解を試み、因数分解出来なかったら、各係数の値を調べて、条件に応じての計算です。
二次方程式になった場合、二次方程式の解法は、因数分解と言えないことは無く、広義の意味合いからは、全てが因数分解の利用により、二つの二元二次方程式の共通の値が求められた事になるのでしょうか。
ペンシル使用因数分解計算は、簡単に楕円の交点の方程式が解けると、記載されたものがありますが、実際にプログラムを組む場合は、四次の連立方程式を組む場合と大差ありませんでした。
三次方程式は、カルダノの方法による三次方程式の解法を使用しています。
三次方程式のプログラムは、埼玉工業大学 工学部 機械工学 小西研究室のWABサイトにあるフリーウェアからダウンロードして、Delphi用に組み直ししました。
プログラムが正しいかどうかは、高精度計算サイトの結果と比較して検証をしました。 元のプログラム、資料は、 "個人の学習以外は、使用できません" とあるので、此処での公開は差し控えさせて頂きます。
必要であれば、前記、WABサイトを直接、訪問してください、インターネットで、検索すれば、すぐに見つかります。

交点の計算時、二つの楕円の軸角がゼロであると、因数分解が出来ない条件が沢山発生します。
因数分解が出来なかったときは a,h,b,f,g,d の値と楕円の二元二次方程式の値から交点の値を求める事が出来ますが、判別が煩雑になります。
最初は計算時の軸角ゼロでチャレンジしましたが、あきらめて、計算時の軸角を33.33--°にして計算していました。
軸角度は、ゼロ度でなければ、計算上桁落ちの無い角度、通常精度の場合は、0.001°以上に設定をすれば、良いようです。
そこで、30°に変更しました。
あらためて軸角度変更なしの時の条件を整理し、軸角ゼロの時でも答えがでるようにしてみました。
次に軸角度を変更した場合としない場合で、因数分解出来ない条件と、因数分解出来ても連立方程式の変更が必要な場合について項目を列記します。
軸角度をゼロ以外にした場合
1. 楕円比が等しくて、軸角も等しい場合
λで導き出した方程式が、二元二次式にならず、二元一次式になります、因数分解は出来せん。
この場合は、この二元一次式と、どちらかの楕円の二元二次式の連立方程式の解法を行います。
軸角度を変更しない場合
次の条件が、軸角度を変更した場合に対して追加になります。
二つの楕円の軸角がゼロ度の時に発生します。
1.水平移動(因数分解可 連立方程式の変更)
2.垂直移動(因数分解可 連立方程式の変更)
3.同軸 計算基準楕円が a > b の時
4.同軸 計算基準楕円が b > a の時
5. 楕円比が等しく水平移動
6. 楕円比が等しく垂直移動
7. 軸角がゼロではないが、微小角(0.001°以下)の時
上記項目の1,2は、因数分解は出来るのですが、β の値がゼロの時の計算です。
7は、桁落ちによるもので、精度よく交点を求めるのには多倍長演算が必須の様です。
プログラム
 左図赤印の中に、因数分解の因の字が表示された場合は、因数分解の使用により交点がもとめられた場合で、単なる〇が表示された場合は、因数分解をしていません。
左図赤印の中に、因数分解の因の字が表示された場合は、因数分解の使用により交点がもとめられた場合で、単なる〇が表示された場合は、因数分解をしていません。
計算は次のように値を変更して計算し、最後に角度の丸め以外、元へ戻して結果の表示をしています。
楕円1を原点に移動。
楕円比の大きい方の軸角が30°になるよう座標軸角変更
楕円の最大半径を200にスケール設定
軸角度の変更を行わない場合、軸角は0.001°以下を丸め。
半径差が0.002以下の場合は円として、大きい方の半径を使用
(角度、半径差、多倍長演算時はもっと小さい値を指定します。)
四次方程式を利用した時、軸角を30°にしたので、此処でも30°にしました。
30°でなくても、ゼロ度でなければ基本的に問題ありません。
座標の変更は、計算の桁数を下げる効果があるので、座標の原点への移動はした方が良いようです。
プログラムの中に、沢山コメントが記載してあるので、それを参照してください。
プログラムの計算結果について、出来る限り沢山のパターンの確認をしましたが、全てのパターンをテスト出来ていると確信は持てません。
問題があった場合は、修正をお願いします。
double の精度では、計算途中での桁落ちの影響が大きく、微小角での値は正しく計算されません。
色々な計算のパターンを試してみましたが、ギリギリ Extendedの精度でそれなりの答えが得られるようです。
色々な場合で、桁落ちの為の対策が必要で、全ての条件での桁落ち対策をすることは困難なようです。
計算時の軸角をゼロ度以外にすることにより、楕円比が等しい時以外は、因数分解により交点を求めることが出来るようになりました。
しかし、計算精度が、extended でも、64ビットでコンパイルすると精度がDoubleになってしまうので注意が必要です。
λ
の値は、条件によって、実数解が一個になる場合と三個になる場合がありますが、必ず実数解になる λ1
を使用すれば、交点を得ることが出来ます。
λ2, λ3 でも実数解になれば、同じ交点が計算できます。
安定した結果が必要な場合は、四次、二次方程式の解法による方法が良いでしょう。
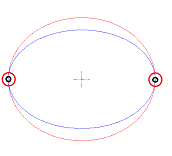
左図のような接線になるような場合、extended
でも精度が不足するようです。
小数点以下、二桁程度の精度しか出せません、高い精度が必用な場合、多倍長演算が必要なようです。
三次方程式の解法後 λ
の値で、楕円1と楕円2 x λ の差分をとりますが、λ の値のわずかな差で交点の座標に大きな差が出ます。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.ExtCtrls, Vcl.StdCtrls, Vcl.Buttons, math;
type
TELLIPSE = record
fRad_X : Extended; // X 方向半径
fRad_Y : Extended; // Y 方向半径
fAngle : Extended; // 楕円角度
fCx : Extended; // 楕円中心位置 X
fcy : Extended; // 楕円中心位置 Y
startAngle : Extended; // 開始角
endAngle : Extended; // 終了角
end;
Tarray3x3 = array[1..3] of array[1..3] of Extended;
TForm1 = class(TForm)
Panel1: TPanel;
Ellipse1Box: TGroupBox;
radius_a1_Edit: TLabeledEdit;
radius_b1_Edit: TLabeledEdit;
Center_x1_Edit: TLabeledEdit;
Center_y1_Edit: TLabeledEdit;
angle_q1_Edit: TLabeledEdit;
Ellipse2Box: TGroupBox;
radius_a2_Edit: TLabeledEdit;
radius_b2_Edit: TLabeledEdit;
Center_x2_Edit: TLabeledEdit;
Center_y2_Edit: TLabeledEdit;
angle_q2_Edit: TLabeledEdit;
Panel2: TPanel;
SelectBtn: TBitBtn;
Image1: TImage;
End_angle_E2: TLabeledEdit;
Start_angle_S2: TLabeledEdit;
Start_angle_S1: TLabeledEdit;
End_angle_E1: TLabeledEdit;
Timer1: TTimer;
Button1: TButton;
CheckBox1: TCheckBox;
procedure FormCreate(Sender: TObject);
procedure SelectBtnClick(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
procedure imageClear;
function Dist(x1, y1, x2, y2 : Extended): Extended ;
function Angle(dx, dy: Extended): Extended ;
procedure LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
procedure pitchControl(NLine, LW: integer);
procedure LineSubPitch(Tcv : TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2: Extended);
function angleSe(a, b, rad: Extended): Extended;
procedure EllipseEx(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
procedure quadratic_transform(a, b, x, y, qdeg: Extended; var A0, B0, C0, D0, E0, F0: Extended);
procedure determinant(a, b, c, d, e, f: Extended; var arrayf: Tarray3x3);
procedure difference0(a1, a2, a3, b1, b2, b3: Extended; var ah03, ah02, ah01, ah00: Extended; addF: boolean);
function cubicequation(a, b, c, d: Extended; var cub2, cub1, cub0: Extended): byte;
procedure inputdata_drawing;
procedure cross_calc;
function difference1(arr1, arr2: Tarray3x3; var ah03, ah02, ah01, ah00: Extended): Extended;
procedure difference2(arr1, arr2: Tarray3x3; var arr3: Tarray3x3);
function difference3(arr3: Tarray3x3; var a, h, b, g, f, c: Extended): Extended;
function factorization(a, h, b, g, f, c: Extended; var alf1, bta1, gam1, alf2, bta2, gam2: Extended): boolean;
function factorization2(a, h, b, g, f, c: Extended; var ar, alfa: Extended): boolean;
function quadratic(A, B, C, D, E, F, a1, b1, g1: Extended; var x1, x2: Extended): byte;
function quadratic4(A1, B1, C1, D1, E1, F1, g, f, c: Extended; var x1, x2: Extended): boolean;
procedure StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: Extended; sf: boolean);
function intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: Extended): boolean;
function angle_amendment(angle : Extended): Extended;
function angle180_amendment(angle : Extended): Extended;
function quadratic_equation(a, b, c: Extended; var x1, x2: extended): boolean;
function quadratic5(a1, b1, c1, d1, e1, f1, z1, z2: Extended; flag: boolean; var m1, m2, m3, m4: Extended): byte;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
const
PitchN = 5; // 線ピッチ設定数
LineN = 3; // 線種数
LIMIT8 = 0.00000001;
type
TLinePitch = Record // 線種用レコード
Pitch : array[0..PitchN] of Extended; // ピッチ 線長さ 空白の繰り返し
segment : integer; // ピッチ数
End;
var
LPitch : array of TLinePitch; // 線種用 (線ピッチ)
VPitch : array[0..PitchN] of Extended; // 線幅による線ピッチ設定用
magnification : Extended;
ar1, ar2 : Extended;
br1, br2 : Extended;
xo1, xo2 : Extended;
yo1, yo2 : Extended;
Ellipse1 : TELLIPSE; // 楕円1
Ellipse2 : TELLIPSE; // 楕円2
shift_x : Extended;
shift_y : Extended;
scale : Extended;
xshift : Extended;
yshift : Extended;
d01 : Extended;
d0p : integer;
ZeroAngleF : boolean; // 楕円選択フラグ
TimerF : Boolean;
const
draw_margin = 30; // 左右上下作図マージン
procedure TForm1.imageClear;
begin
image1.Canvas.Brush.Style := bsSolid;
image1.Canvas.Brush.Color := clWhite;
image1.Canvas.FillRect(Rect(0, 0, image1.Width, image1.Height));
end;
//-----------------------------------------------
// 線幅によるピッチの補正
// 線幅を広くするとスペースが狭くなるので広げます
// NLine 線種
// LW 線幅
//-----------------------------------------------
procedure TForm1.pitchControl(NLine, LW: integer);
var
i : integer;
begin
// 線幅によるピッチの補正
for i := 0 to pitchN do begin
if i mod 2 <> 0 then // 奇数配列noセグメントがスペース
Vpitch[i] := LPitch[NLine].Pitch[i] + LW // スペースに線幅加算
else
Vpitch[i] := LPitch[NLine].Pitch[i];
end;
end;
//----------------------------
// 作図用 二点間線引き
//----------------------------
procedure TForm1.LineSub(Tcv: TCanvas; px1, py1, px2, py2: Extended);
var
x1, y1, x2, y2 : integer ;
begin
x1 := Round(px1);
y1 := Round(py1);
x2 := Round(px2);
y2 := Round(py2);
Tcv.MoveTo(x1, y1);
Tcv.LineTo(x2, y2);
end;
//----------------------
// 距離(長さ)を計算
// x1, y1 : 始点
// x2, y2 : 終点
// out : 距離(長さ)
//----------------------
function TForm1.Dist(x1, y1, x2, y2 : Extended): Extended ;
begin
Result := Sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) ;
end;
//--------------------------------
// 角度を計算[rad]
// dx : X方向差分
// dy : Y方向差分
// out: 角度 (0~2 * Pi)
//--------------------------------
function TForm1.Angle(dx, dy: Extended): Extended ;
var
r : Extended ;
begin
Result := 0.0;
if (Abs(dx) < LIMIT8) and (Abs(dy) < LIMIT8) then exit;
r := ArcTan2(dy, dx);
if r < 0.0 then r := r + 2.0 * Pi;
Result := r;
end;
//--------------------------------------
// 線分の表示・サブ2:線種指定
// Ln : 線種番号(1-)
// i : 開始セグメント番号(終了時更新)
// d1 : 開始ピッチ長さ (終了時更新)
// px1, py1 : 線分始点[mm]
// px2, py2 : 線分終点[mm]
//--------------------------------------
procedure TForm1.LineSubPitch(Tcv: TCanvas; Ln: integer; var i: integer; var d1: Extended; px1, py1, px2, py2: Extended);
var
x1, y1, x2, y2 : Extended;
a, sa, ca, d, p : Extended;
PenStyle : TPenstyle;
begin
PenStyle := Tcv.Pen.Style; // 線種バックアップ
Tcv.Pen.Style := psSolid;
if (Ln < 0) or (Ln >= LineN) then begin // 無い線種は実線
LineSub(Tcv, px1, py1, px2, py2);
Tcv.Pen.Style := PenStyle; // 線種戻し
exit;
end;
a := Angle(px2 - px1, py2 - py1); // 角度計算
d := Dist(px1, py1, px2, py2); // 距離計算
ca:= Cos(a); // コサイン
sa:= Sin(a); // サイン
x1:= px1; // 始点x
y1:= py1; // 始点y
repeat
p := Vpitch[i] - d1; // ピッチと開始ピッチ長さ差分 残り分
if (p > d) then p := d; // 距離より残り分が大きい場合 距離
x2 := x1 + p * ca; // 新しい位置計算
y2 := y1 + p * sa;
if (i mod 2) = 0 then // セグメント偶数毎に線引き 空白部線引きしない
LineSub(Tcv, x1, y1, x2, y2);
x1 := x2; // 終点を始点にセット
y1 := y2;
d := d - p ; // 残り長さ計算
if d > LIMIT8 then begin // 残り長さがあったら
d1 := 0.0; // 開始ピッチ長さクリア
Inc(i); // セグメントカウンターインクリメント
if i >= LPitch[Ln].segment then i := 0; // セグメント数を超えたらゼロに戻し
end;
until d <= LIMIT8;
d1 := d1 + p; // 開始ピッチ長さ
Tcv.Pen.Style := PenStyle; // 線種戻し
end;
//------------------------------------------
// 楕円の開始角を 基礎円の開始角に変換
//------------------------------------------
function TForm1.angleSe(a, b, rad: Extended): Extended;
const
KMIN = 0.00000001;
var
l : Extended;
begin
// 90°, 270°, 0°, 180° 360°近傍は計算しない
if (abs(rad - pi / 2) < KMIN) or (abs(rad - pi - pi / 2) < KMIN)
or (abs(rad) < KMIN) or (abs(rad - pi) < KMIN) or
(abs(rad - pi * 2) < KMIN)
then begin
result := rad;
exit;
end;
// 底辺の長さ計算 ( b / a の値がいつも正の値なので元の角度によって角度を補正)
// 分母がゼロに近くなる時もあるので、判別が不要なarctan2を使用します
l := b / a / tan(rad);
// 180°以下だったら
if rad < pi then
result := arctan2(1, l)
else
// 360°以下だったら
if rad < pi * 2 then
result := arctan2(1, l) + pi
// 360°を超えていたら
else
result := arctan2(1, l) + pi * 2;
end;
//---------------------------------------
// 楕円の描画
// Windows為ののy方向変換は,このルーチンで行います。
// tcv 描画キャンバスの指定
// h キャンバスの高さ
// lf 線の種類
// lw 線の幅
// lc 線の色
// a 半径a
// b 半径b
// x 中心位置 x
// y 中心位置 y
// rq 楕円の角度
// sq 描画開始角
// eq 描画終了
//---------------------------------------
procedure TForm1.EllipseEx(Tcv : TCanvas; h, lf, lw: integer; lc: Tcolor; a, b, x, y, rq, sq, eq: Extended);
var
sqrad, eqrad : Extended;
qrad : Extended;
Ssqrad, Seqrad : Extended;
sp : integer;
dq : Extended;
d1 : Extended;
dp : integer;
xf, yf : Extended;
rdist, nrad : Extended;
px1, py1 : Extended;
px2, py2 : Extended;
i : integer;
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// y方向変換
y := h - y;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// 終了角と開始角が一致したら全周
if abs(sq - eq) < LIMIT8 then begin
sq := 0;
eq := 360;
end;
sp := round(sqrt(a + b) * 4); // 分割数
// 楕円の計算と描画
sqrad := sq / 180 * pi;
eqrad := eq / 180 * pi;
qrad := pi / 180 * rq; // 回転角 ラジアン
Ssqrad := angleSe(a, b, sqrad); // 基本円角度に変換
Seqrad := angleSe(a, b, eqrad); // 基本円角度に変換
// 分割微小角計算 分割数角度で補正
if Seqrad >= Ssqrad then begin
sp := round(sp * (Seqrad - Ssqrad) / pi);
if sp = 0 then sp := 1;
dq := (Seqrad - Ssqrad) / sp // 分割微小角 ラジアン
end
else begin
sp := round(sp * (Pi * 2 - Ssqrad + Seqrad) / pi);
if sp = 0 then sp := 1;
dq := (Pi * 2 - Ssqrad + Seqrad) / sp; // 分割微小角 ラジアン
end;
// 開始点の計算
d1 := 0; // 長さ
dp := 0; // セグメント位置
xf := cos(Ssqrad) * a; // 基本楕円座標X スタート座標
yf := sin(Ssqrad) * b; // 基本楕円座標y スタート座標
nrad := arctan2(yf, xf) + qrad; // 新しい角度 回転角加算
rdist := sqrt(xf * xf + yf * yf); // 中心と楕円座標の距離
px1 := cos(nrad) * rdist + x; // 開始座標X
py1 := sin(nrad) * -rdist + y; // 開始座標Y -rdistはY座標反転の為
// WindowはY座標方向が逆のため
// 分割数分計算繰り返し描画
for i := 1 to sp do begin
xf := cos(Ssqrad + dq * i) * a;
yf := sin(Ssqrad + dq * i) * b;
nrad := arctan2(yf , xf) + qrad;
rdist := sqrt(xf * xf + yf * yf);
px2 := round(cos(nrad) * rdist + x); // 終点座標X
py2 := round(sin(nrad) * -rdist + y); // 終点座標Y
// ピッチ線描画
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
dp, // セグメント位置
d1, // 長さ
px1, // 始点X
py1, // 始点Y
px2, // 終点X
py2 // 終点Y
);
px1 := px2; // 終点Xを始点Xに
py1 := py2; // 終点Yを始点Yに
end;
end;
//-------------------------------------------------------------
// 直線の描画
// 直線の開始はsfをTrueにします。
// つながった直線、折れ線を描画する場合は、sfをFalseに
//-------------------------------------------------------------
procedure TForm1.StraightLineDraw(Tcv: TCanvas; h, lf, lw: integer; lc: Tcolor; xs, ys, xe, ye: Extended; sf: boolean);
begin
Tcv.Pen.Width := lw;
Tcv.Pen.Color := lc;
// 線幅によるピッチの補正
pitchControl(lf, lw);
// y方向変換
ys := h - ys;
ye := h - ye;
if sf then begin
d01 := 0;
d0p := 0;
end;
LineSubPitch( // ピッチ線描画
tcv, // TCanvas
lf, // 線種
d0p, // セグメント位置
d01, // 長さ
xs, // 始点X
ys, // 始点Y
xe, // 終点X
ye // 終点Y
);
end;
//-------------------------------------------------
// 楕円の方程式 二次方程式への変換
// AX^2 + BXY + CY^2 + DX + EY + F の A,B,C,D,E,F
//-------------------------------------------------
procedure TForm1.quadratic_transform(a, b, x, y, qdeg: Extended; var A0, B0, C0, D0, E0, F0: Extended);
var
Q : Extended;
sin_Q, cos_q : Extended;
begin
Q := qdeg / 180 * pi; // ラジアン単位に変換
sin_Q := sin(Q);
cos_Q := cos(Q);
A0 := cos_Q * cos_Q / a / a + sin_Q * sin_Q / b / b;
B0 := 2 * (1 / a / a - 1 / b / b) * sin_Q * cos_Q;
C0 := sin_Q * sin_Q / a / a + cos_Q * cos_Q / b / b;
D0 := -2 * ((x * cos_Q * cos_Q + y * sin_Q * cos_Q) / a / a + (x * sin_Q * sin_Q - y * sin_Q * cos_Q) / b / b);
E0 := -2 * ((x * sin_Q * cos_Q + y * sin_Q * sin_Q) / a / a + (y * cos_Q * cos_Q - x * sin_Q * cos_Q) / b / b);
F0 := (x * x * cos_Q * cos_Q + 2 * x * y * sin_Q * cos_Q + y * y * sin_Q * sin_Q) / a / a
+ (x * x * sin_Q * sin_Q - 2 * x * y * sin_Q * cos_Q + y * y * cos_Q * cos_Q) / b / b
- 1;
end;
//----------------------
// 3×3 行列式への変換
//----------------------
procedure TForm1.determinant(a, b, c, d, e, f: Extended; var arrayf: Tarray3x3);
begin
arrayf[1, 1] := a;
arrayf[1, 2] := b / 2;
arrayf[1, 3] := d / 2;
arrayf[2, 1] := b / 2;
arrayf[2, 2] := c;
arrayf[2, 3] := e / 2;
arrayf[3, 1] := d / 2;
arrayf[3, 2] := e / 2;
arrayf[3, 3] := f;
end;
//------------------------
// 三次方程式への変換サブ
//------------------------
procedure TForm1.difference0(a1, a2, a3, b1, b2, b3: Extended; var ah03, ah02, ah01, ah00: Extended; addF: boolean);
var
ah13, ah12, ah11, ah10: extended;
begin
ah13 := - b1 * b2 * b3; // α^3
ah12 := a3 * b1 * b2 + a2 * b1 * b3 + a1 * b2 * b3; // α^2
ah11 := -(a2 * a3 * b1 + a1 * a3 * b2 + a1 * a2 * b3); // α^1
ah10 := a1 * a2 * a3; // c
if addF then begin
ah03 := ah03 + ah13;
ah02 := ah02 + ah12;
ah01 := ah01 + ah11;
ah00 := ah00 + ah10;
end
else begin
ah03 := ah03 - ah13;
ah02 := ah02 - ah12;
ah01 := ah01 - ah11;
ah00 := ah00 - ah10;
end;
end;
//---------------------------------------
// 二元二次行列連立式の三次方程式への変換
//---------------------------------------
function TForm1.difference1(arr1, arr2: Tarray3x3; var ah03, ah02, ah01, ah00: Extended): Extended;
begin
ah03 := 0;
ah02 := 0;
ah01 := 0;
ah00 := 0;
difference0(arr1[1, 1], arr1[2, 2], arr1[3, 3],
arr2[1, 1], arr2[2, 2], arr2[3, 3], ah03, ah02, ah01, ah00, true);
difference0(arr1[1, 2], arr1[2, 3], arr1[3, 1],
arr2[1, 2], arr2[2, 3], arr2[3, 1], ah03, ah02, ah01, ah00, true);
difference0(arr1[1, 3], arr1[2, 1], arr1[3, 2],
arr2[1, 3], arr2[2, 1], arr2[3, 2], ah03, ah02, ah01, ah00, true);
difference0(arr1[1, 3], arr1[2, 2], arr1[3, 1],
arr2[1, 3], arr2[2, 2], arr2[3, 1], ah03, ah02, ah01, ah00, False);
difference0(arr1[1, 2], arr1[2, 1], arr1[3, 3],
arr2[1, 2], arr2[2, 1], arr2[3, 3], ah03, ah02, ah01, ah00, False);
difference0(arr1[1, 1], arr1[2, 3], arr1[3, 2],
arr2[1, 1], arr2[2, 3], arr2[3, 2], ah03, ah02, ah01, ah00, False);
Result := ah03 + ah02 + ah01 + ah00;
end;
//---------------------
// 3×3行列式の差計算
//---------------------
procedure TForm1.difference2(arr1, arr2: Tarray3x3; var arr3: Tarray3x3);
var
i, k: integer;
begin
for i := 1 to 3 do
for k := 1 to 3 do begin
arr3[i, k] := arr1[i, k] - arr2[i, k]; // 差分計算
// if abs(arr3[i, k]) < 1E-16 then arr3[i, k] := 0; // 1E-14より小さかったらゼロ
end;
// デバッグの為上から分離 因数分解と二次一次の計算境目設定確認の為 y 又は x 移動 0.001 近辺
// 1E-16 程度で、これより小さくすると、倍精度で因数分解とそうでない場合の境目で大きな誤差が
// 発生するようです。 Extended で 1E-16 程度
// もっと小さくして精度を上げるためには、多倍長演算が必要なようです。
for i := 1 to 3 do
for k := 1 to 3 do begin
if abs(arr3[i, k]) < 1E-16 then arr3[i, k] := 0; // 1E-16より小さかったらゼロ
end;
end;
//-----------------------------
// 3×3行列式det の計算
// 因数分解用方程式値の取り出し
//-----------------------------
function TForm1.difference3(arr3: Tarray3x3; var a, h, b, g, f, c: Extended): Extended; // detの計算
var
a1, a2, a3 : Extended;
b1, b2, b3 : Extended;
begin
a1 := arr3[1, 1] * arr3[2, 2] * arr3[3, 3];
a2 := arr3[1, 2] * arr3[2, 3] * arr3[3, 1];
a3 := arr3[1, 3] * arr3[2, 1] * arr3[3, 2];
b1 := arr3[1, 3] * arr3[2, 2] * arr3[3, 1];
b2 := arr3[2, 3] * arr3[3, 2] * arr3[1, 1];
b3 := arr3[3, 3] * arr3[1, 2] * arr3[2, 1];
result := a1 + a2 + a3 - b1 - b2 - b3;
a := arr3[1, 1]; // ax^2 二元二次方程式変換
h := arr3[1, 2]; // 2hxy
b := arr3[2, 2]; // by^2
g := arr3[1, 3]; // 2gx
f := arr3[2, 3]; // 2fy
c := arr3[3, 3]; // c
end;
//--------------------------------------------------------------------
// 三次方程式の解法 カルダノの方法
// 実数解の値の時 byte ビット0 ビット 1 ビット2 をそれぞれ1にします
//--------------------------------------------------------------------
function TForm1.cubicequation(a, b, c, d: Extended; var cub2, cub1, cub0: Extended): byte;
const
MINIMAMD = 1E-6; // Double 時
MINIMAME = 1E-8; // Extended 時
KC = 1E-17; // Double Extended 判別用
MINIMAD = 1E-16; // Double 時
MINIMAE = 1E-20; // Extended 時
var
DECheck : Extended;
MINIDE : Extended;
MINDE : Extended;
A2, A1, A0 : Extended;
e1, e0, e1s3, e0s2, e02s4, e13s27 : Extended;
e02s4pe13s27 : Extended;
xim1, xim2, xim3 : string;
ru, rv, ruh1s3, rvh1s3 : Extended;
Qu, Qv, Qus3, Qvs3 : Extended;
u1, u2, u3, v1, v2, v3 : Extended;
u1pv1, u2pv3, u3pv2 : Extended;
u1S, u2S, u3S, v1S, v2S, v3S : Extended;
u1pv1S, u2pv3S, u3pv2S : Extended;
begin
result := 0;
if a = 0 then exit;
MINIDE := MINIMAME; // 誤差をExtdedに設定
DECheck := 1 + KC; // 誤差判別値セット
if DECheck = 1 then begin
MINIDE := MINIMAMD; // 桁落ち確認 桁落ちしたら Doubel に設定
MINDE := MINIMAD;
end;
// x^3 + A2x^2 + A1x + A0
A2 := b / a;
A1 := c / a;
A0 := d / a;
e1 := -A2 * A2 / 3 + A1;
e0 := 2 / 27 * A2 * A2 * A2 - A2 * A1 / 3 + A0;
e1s3 := e1 / 3;
e0s2 := e0 / 2;
e02s4 := e0s2 * e0s2;
e13s27 := e1s3 * e1s3 * e1s3;
e02s4pe13s27 := e02s4 + e13s27; // 判別値
if abs(e02s4pe13s27) < MINDE then e02s4pe13s27 := 0;
if e02s4pe13s27 >= 0 then begin // ru rv に負数が存在
ru := -e0s2 + sqrt(e02s4pe13s27);
rv := -e0s2 - sqrt(e02s4pe13s27);
Qu := 0;
end
else begin // ru rv に負数存在なし
ru := sqrt(e02s4 + ABS(e02s4pe13s27));
rv := ru;
Qu := arcCos(-e0s2 / ru);
end;
if ru < 0 then begin // ru負数時の立方根対策
ru := -ru;
ruh1s3 := power(ru, 1/3);
ruh1s3 := -ruh1s3;
end
else
ruh1s3 := power(ru, 1/3);
if rv < 0 then begin // rv負数時の立方根対策
rv := -rv;
rvh1s3 := power(rv, 1/3);
rvh1s3 := -rvh1s3;
end
else
rvh1s3 := power(rv, 1/3);
Qv := -Qu;
Qus3 := Qu / 3;
Qvs3 := Qv / 3;
// 実数部の計算
u1 := ruh1s3 * cos(Qus3);
u2 := ruh1s3 * cos(Qus3 + 2 / 3 * pi);
u3 := ruh1s3 * cos(Qus3 + 4 / 3 * pi);
v1 := rvh1s3 * cos(Qvs3);
v2 := rvh1s3 * cos(Qvs3 + 2 / 3 * pi);
v3 := rvh1s3 * cos(Qvs3 + 4 / 3 * pi);
u1pv1 := u1 + v1;
u2pv3 := u2 + v3;
u3pv2 := u3 + v2;
cub2 := u1pv1 - A2 / 3;
cub1 := u2pv3 - A2 / 3;
cub0 := u3pv2 - A2 / 3;
// 虚数部の計算
u1S := ruh1s3 * sin(Qus3);
u2S := ruh1s3 * sin(Qus3 + 2 / 3 * pi);
u3s := ruh1s3 * sin(Qus3 + 4 / 3 * pi);
v1S := rvh1s3 * sin(Qvs3);
v2S := rvh1s3 * sin(Qvs3 + 2 / 3 * pi);
v3S := rvh1s3 * sin(Qvs3 + 4 / 3 * pi);
u1pv1S := u1S + v1S;
u2pv3S := u2S + v3S;
u3pv2S := u3S + v2S;
if abs(u1pv1S) < MINIDE then u1pv1S := 0; // 誤差許容値 MINIMAM 計算誤差対策
if abs(u2pv3S) < MINIDE then u2pv3S := 0; // 虚数部が指定値以下にら
if abs(u3pv2S) < MINIDE then u3pv2S := 0; // 虚数部をゼロとみなします
if u1pv1S <> 0 then xim1 := floattostrF(u1pv1S, ffFixed, 10, 5) + ' i'
else begin
xim1 := '';
result := result or 1;
end;
if u2pv3S <> 0 then xim2 := floattostrF(u2pv3S, ffFixed, 10, 5) + ' i'
else begin
xim2 := '';
result := result or 2;
end;
if u3pv2S <> 0 then xim3 := floattostrF(u3pv2S, ffFixed, 10, 5) + ' i'
else begin
xim3 := '';
result := result or 4;
end;
with Form1.Image1.Canvas do begin
TextOut(20, 0,'λ1= ' + floattostrF(cub2, ffFixed, 15, 10) + ' ' + xim1);
TextOut(20, 20,'λ2= ' + floattostrF(cub1, ffFixed, 15, 10) + ' ' + xim2);
TextOut(20, 40,'λ3= ' + floattostrF(cub0, ffFixed, 15, 10) + ' ' + xim3);
end;
end;
//---------------------------------------
// 因数分解サブルーチン ルートの中の処理
//---------------------------------------
function TForm1.factorization2(a, h, b, g, f, c: Extended; var ar, alfa: Extended): boolean;
const
MINIMAMD = 1E-16; // Double 時 2018/11/16
MINIMAME = 1E-18; // Extended 時
KC = 1E-17; // Double Extended 判別用
MINICD = 1E-12; // Double 時
MINICE = 1E-16; // Extended 時
var
DECheck, MINIDE, MINIC: Extended;
a0, b0, c0 : Extended;
f0 : Extended;
begin
MINIDE := MINIMAME; // 誤差をExtdedに設定
MINIC := MINICE;
DECheck := 1 + KC; // 誤差判別値セット
if DECheck = 1 then begin
MINIDE := MINIMAMD; // 桁落ち確認 桁落ちしたら Doubel に設定
MINIC := MINICD;
end;
result := true;
a0 := h * h - a * b; // a0の値がかなり小さくなるのでこの値が
b0 := (g * h - a * f) * 2; // あまり小さくなると因数分解計算の誤差が大きくなります
c0 := g * g - a * c; // 行列式の差分計算時のゼロ判定値によって最小値が変わります
if c0 < 0 then
if abs(c0) < MINC then c0 := 0; // -17 -> -16
if abs(a0) < 1E-28 then a0 := 0;
if a0 < 0 then
if abs(a0) < MINIDE then a0 := 0;
if (a0 < 0) or (c0 < 0) then begin // a0 又は c0がマイナスの時は複素数となりルート不可
result := false;
exit;
end;
f0 := b0 * b0 - 4 * a0 * c0; // ルートの中の二次方程式の中のルートの中の計算
if abs(f0) < 1E-11 then f0 := 0; // マイナスでも値が小さければ誤差としてゼロにします
if (a0 >= 0) and (f0 = 0) then begin // f0 がゼロならルートを開けます
ar := sqrt(a0); // a0 がゼロでも可能ですが βがゼロになることがあるで
alfa := sqrt(c0); // 因数分解値による連立方程式の為 a0(y^2)がゼロの時
if b0 < 0 then alfa := -alfa; // 因数分解NGとしています a0(y^2)がゼロに近くなると
end // 誤差も大きくなります。
else // βがゼロの時の方程式を作成すれば a0 がゼロでもOK
result := false;
end;
//-----------------------------------------------------------------------------------------------
// 因数分解
// a がゼロの時は因数分解できません。
// (α1x + β1y + γ1)(α2x + β2y + γ2)
//-----------------------------------------------------------------------------------------------
function TForm1.factorization(a, h, b, g, f, c: Extended; var alf1, bta1, gam1, alf2, bta2, gam2: Extended): boolean;
var
ar, alfa: Extended;
begin
result := false;
// detの計算 ゼロでないと因数分解できません
ar := a * b * c - a * f * f - b * g * g - c * h * h + 2 * f * g * h;
// 因数分解出来なければ終了
if abs(ar) > 1E-12 then exit; // 1E-12 誤差許容値
if abs(a) < 1E-30 then exit; // a がゼロの時は因数分解不可 1E-12 -> 1E-30
result := factorization2(a, h, b, g, f, c, ar, alfa);
if result then begin
alf1 := a;
bta1 := h - ar;
gam1 := g - alfa;
alf2 := 1;
bta2 := (h + ar) / a;
gam2 := (g + alfa) / a;
end;
end;
//----------------------------------------------------------------------------------------
// 連立方程式の解法 交点 X, Y を求めます
// 因数分解できた場合の処理
// 因数分解値一次式と楕円二元二次式の連立方程式の解法
function TForm1.quadratic(A, B, C, D, E, F, a1, b1, g1: Extended; var x1, x2: Extended): byte;
const
MINIMAMD = 1E-9; // Double 時
MINIMAME = 1E-10; // Extended 時
KC = 1E-17; // Double Extended 判別用
var
a0, b0, c0 : Extended;
f0 : Extended;
m, n: Extended;
MIN, DECheck: Extended;
begin
MIN := MINIMAME; // 誤差をExtdedに設定
DECheck := 1 + KC; // 誤差判別値セット
if DECheck = 1 then MIN := MINIMAMD; // 桁落ち確認 桁落ちしたら Doubel に設定
result := 0;
if abs(b1) < 1e-23 then exit; // b1の値がゼロだったら答え無し
m := -g1 / b1; // y = m + nx;
n := -a1 / b1;
a0 := A + C * n * n + B * n;
b0 := B * m + D + E * n + 2 * C * m * n;
c0 := E * m + C * m * m + F;
f0 := b0 * b0 - 4 * a0 * c0;
if abs(f0) < MIN then f0 := 0; // 1E-10は誤差の許容値 誤差 ±1E-5
// if (f0 < 0) and (abs(f0) < 1E-10) then f0 := 0; // 1E-10は誤差の許容値 誤差 ±1E-5
if f0 = 0 then result := 1;
if f0 > 0 then result := 2;
if (f0 < 0) or (abs(a0) < 1E-30) then begin // f0 がマイナス a0がゼロなら答え無し
result := 0; // a0がゼロの場合答え無し
exit;
end;
x1 := (-b0 + sqrt(f0)) / a0 / 2;
x2 := (-b0 - sqrt(f0)) / a0 / 2;
end;
// 因数分解できなかった場合の処理4
// 2gx + 2fy + c := 0 の 一次式と楕円二元二次式の連立方程式の解法
function TForm1.quadratic4(A1, B1, C1, D1, E1, F1, g, f, c: Extended; var x1, x2: Extended): boolean;
var
m, n : Extended;
a0, b0, c0, f0: Extended;
begin
result := false;
m := - c / 2 / f;
n := - g / f;
a0 := A1 + B1 * n + C1 * n * n; // x^2
b0 := B1 * m + 2 * C1 * n * m + D1 + E1 * n; // x
c0 := C1 * m * m + E1 * m + F1;
f0 := b0 * b0 - 4 * a0 * c0;
if abs(f0) < 1E-10 then f0 := 0; // 1E-10は誤差の許容値 誤差 ±1E-5
if (f0 >= 0) and (a0 <> 0) then begin
x1 := (-b0 + sqrt(f0)) / 2 / a0;
x2 := (-b0 - sqrt(f0)) / 2 / a0;
result := true;
end;
end;
// 二次方程式の解法
// 座標軸角がゼロの時に使用します。
function TForm1.quadratic_equation(a, b, c: Extended; var x1, x2: extended): boolean;
const
MINIMAMD = 1E-10; // Double 時
MINIMAME = 1E-12; // Extended 時
KC = 1E-17; // Double Extended 判別用
var
f0: double;
MIN, DECheck: Extended;
begin
MIN := MINIMAME; // 誤差をExtdedに設定
DECheck := 1 + KC; // 誤差判別値セット
if DECheck = 1 then MIN := MINIMAMD; // 桁落ち確認 桁落ちしたら Doubel に設定
result := false;
f0 := b * b - 4 * a * c;
if abs(f0) < MIN then f0 := 0;
if f0 < 0 then exit;
x1 := (-b + sqrt(f0)) / 2 / a;
x2 := (-b - sqrt(f0)) / 2 / a;
result := true;
end;
// 楕円二元二次方程式のx 又は yの値が既知の時に二次方程式の解法を行います
// 座標軸角がゼロの時に使用します。
function TForm1.quadratic5(a1, b1, c1, d1, e1, f1, z1, z2: Extended; flag: boolean; var m1, m2, m3, m4: Extended): byte;
var
a, b, c: extended;
begin
// xが既知の場合
result := 0;
if flag then begin
a := c1;
b := e1 + b1 * z1;
c := f1 + a1 * z1 * z1 + d1 * z1;
if quadratic_equation(a, b, c, m1, m2) then result := 1;
b := e1 + b1 * z2;
c := f1 + a1 * z2 * z2 + d1 * z2;
if quadratic_equation(a, b, c, m3, m4) then result := result + 2;
end
// yが既知の場合
else begin
a := a1;
b := d1 + b1 * z1;
c := f1 + c1 * z1 * z1 + e1 * z1;
if quadratic_equation(a, b, c, m1, m2) then result := 4;
b := d1 + b1 * z2;
c := f1 + c1 * z2 * z2 + e1 * z2;
if quadratic_equation(a, b, c, m3, m4) then result := result + 8;
end;
end;
//--------------------------------------------------------------------------
// 二つの楕円の交点計算
// 楕円1の角度が30°になるように座標変換をして計算します。
// 座標軸角度を変更しなくても計算は可能です(チェックボックスで選択します。)
//--------------------------------------------------------------------------
procedure TForm1.cross_calc;
var
i, k : integer;
A1, B1, C1, D1, E1, F1 : Extended;
A2, B2, C2, D2, E2, F2 : Extended;
a, h, b, g, f, c : Extended;
xflag : byte;
oflag : byte;
dflag : byte;
iflag : boolean;
arr1, arr2, arr3, arr4 : Tarray3x3;
ah03, ah02, ah01, ah00 : Extended;
lambda1, lambda2, lambda3 : Extended;
det : Extended;
x1, x2, x3, x4 : Extended;
y1, y2, y3, y4 : Extended;
xx : array[0..3] of Extended;
yy : array[0..3] of Extended;
xy : array[0..3] of byte;
alf1, gam1, bta1, alf2, gam2, bta2: Extended;
// alf3, gam3, bta3, alf4, gam4, bta4: Extended;
// alf5, gam5, bta5, alf6, gam6, bta6: Extended;
ret : boolean;
stn, defQ : Extended;
qb, qn : Extended;
nx, ny : Extended;
xob, yob : Extended;
q1b, q2b : Extended;
// 座標戻し 楕円の角度を元の角度に戻します
procedure xyconvert(var x, y : Extended);
begin
stn := sqrt(x * x + y * y);
qb := arctan2(y, x);
qn := qb - defQ / 180 * pi;
x := cos(qn) * stn;
y := sin(qn) * stn;
end;
// 交点丸表示
procedure EllipseDraw(x, y: Extended);
begin
EllipseEx(image1.Canvas,
image1.Height, 3, 1, clblack,
5, 5,
x * magnification - shift_x + draw_margin,
y * magnification - shift_y + draw_margin,
0, 0, 360);
end;
// 座標データー表示
procedure TextoutXY(x, y: Extended; n, m: integer);
begin
x := (x + xshift) / scale;
y := (y + yshift) / scale;
image1.Canvas.TextOut( 20, 450 + n * 20, 'x' + intTostr(m) + '= ' + floatTostrF(x, ffFixed, 10, 3));
image1.Canvas.TextOut(220, 450 + n * 20, 'y' + intTostr(m) + '= ' + floatTostrF(y, ffFixed, 10, 3));
end;
// 因数分解の必要なく方程式の解法可能な場合
// 三次式解法が出来ても此処で計算しないと答えが出ない場合があります
procedure HV_Move;
begin
// 二つの楕円の縦横比が等しい場合
if (abs(a) < 1E-12) and (abs(h) < 1E-12) and (abs(b) < 1E-12) and (g <> 0) and (f <> 0) and (c <> 0) then begin
// 2gx + 2fy + c := 0 の 一次式と楕円二元二次式の連立方程式の解法
ret := quadratic4(A1, B1, C1, D1, E1, F1, g, f, c, x1, x2);
if ret then begin
y1 := - c / 2 / f - g / f * x1;
y2 := - c / 2 / f - g / f * x2;
dflag := 3;
end;
end;
end;
begin
// 座標変換角度 楕円比の大きいほうの軸角の計算角度を30°に設定します
// 座標原点は楕円1を0,0で変化しません
// 半径の差が0.002以下だったら同じにします(大きい方の半径を採用します)
if abs(ar1 - br1) <= 0.002 then
if ar1 >= br1 then br1 := ar1
else ar1 := br1;
if abs(ar2 - br2) <= 0.002 then
if ar2 >= br2 then br2 := ar2
else ar2 := br2;
// 楕円比計算
if ar1 >= br1 then q1b := ar1 / br1
else q1b := br1 / ar1;
if ar2 >= br2 then q2b := ar2 / br2
else q2b := br2 / ar2;
// 楕円比フラグセット
ZeroAngleF := False;
if q2b > q1b then ZeroAngleF := true;
// 楕円の角度処理
q1b := Ellipse1.fAngle;
q2b := Ellipse2.fAngle;
q1b := angle180_amendment(q1b);
q2b := angle180_amendment(q2b);
// 円の場合は角度0°
if ar1 = br1 then q1b := 0;
if ar2 = br2 then q2b := 0;
// 座標変換角度設定
defQ := 0;
if not checkbox1.Checked then begin
if ZeroAngleF then
defQ := 30 - q2b // 100/3-q2b -> 30 - q2b
else
defQ := 30 - q1b; // 100/3-q1b -> 30 - q1b
end;
q1b := q1b + defQ;
q2b := q2b + defQ;
q1b := angle180_amendment(q1b);
q2b := angle180_amendment(q2b);
nx := xo2;
ny := yo2;
// 楕円同士の角度
qb := arctan2(ny, nx);
// 計算上の楕円同士の角度
qn := qb + defQ / 180 * pi;
// 楕円の中心距離
stn := sqrt(nx * nx + ny * ny);
// 計算上の楕円2の中心座標
xob := cos(qn) * stn;
yob := sin(qn) * stn;
// 計算上の楕円角度表示
image1.Canvas.TextOut(580, 500, 'q1b ' + floatTostrF(q1b, ffFixed, 10, 4));
image1.Canvas.TextOut(580, 520, 'q2b ' + floatTostrF(q2b, ffFixed, 10, 4));
// 楕円式の変換
quadratic_transform(ar1, br1, xo1, yo1, q1b, A1, B1, C1, D1, E1, F1);
quadratic_transform(ar2, br2, xob, yob, q2b, A2, B2, C2, D2, E2, F2);
// テスト計算用サンプルデーター
// a1 := 2; b1 := 0; c1 := 4; d1 := -4; e1 := -8; f1 := 3;
// a2 := 1; b2 := 0; c2 := 1; d2 := -2; e2 := 2; f2 := 1;
// a1 := 2; b1 := 0; c1 := 4; d1 := 0; e1 := 0; f1 := -3;
// a2 := 1; b2 := 0; c2 := 1; d2 := 0; e2 := 0; f2 := -1;
// a1 := 7; b1 := 11; c1 := -6; d1 := -9; e1 := -1; f1 := 2;
// a2 :=23; b2 := 24; c2 := -8; d2 := -21; e2 :=-10; f2 :=-74;
determinant(A1, B1, C1, D1, E1, F1, arr1); // 3x3 行列式に変換
determinant(A2, B2, C2, D2, E2, F2, arr2); // 3x3 行列式に変換
// 3x3 3x3 α^3 α^2 α c
difference1(arr1, arr2, ah03, ah02, ah01, ah00); // α三次式に変換
// 三次式の解法 α^3 α^2 α c λ1 λ2 λ3
xflag := cubicequation(ah03, ah02, ah01, ah00, lambda1, lambda2, lambda3);
oflag := 0;
dflag := 0;
a := 0;
h := 0;
b := 0;
g := 0;
f := 0;
c := 0;
//-----------------------------------------------------------------------------------------
// 三次式の解法で、実数解 が複数ある場合は因数分解できた最後の値の因数分解値が採用されます。
// 実数解は一個 又は 三個
if xflag and 1 = 1 then begin
for i := 1 to 3 do
for k := 1 to 3 do begin
arr3[i, k] := arr2[i, k] * lambda1; // arr3 = arr2 * λ1
end;
difference2(arr1, arr3, arr4); // arr4 = arr1 - arr3 λ1
// 単に確認のみ 三次方程式の解の使用なので det は ゼロ
det := difference3(arr4, a, h, b, g, f, c); // det = arr4(det)
if abs(det) < 1E-12 then begin
// 因数分解
if factorization(a, h, b, g, f, c, alf1, bta1, gam1, alf2, bta2, gam2) then begin
oflag := 1;
end;
HV_Move;
end;
end;
// 最初の実数解のみ使用
{
if xflag and 2 = 2 then begin
for i := 1 to 3 do
for k := 1 to 3 do begin
arr3[i, k] := arr2[i, k] * lambda2; // arr3 = arr2 * λ2
end;
difference2(arr1, arr3, arr4); // arr4 = arr1 - arr3 λ2
det := difference3(arr4, a, h, b, g, f, c);
if abs(det) < 1E-12 then begin
// 因数分解
if factorization(a, h, b, g, f, c, alf3, bta3, gam3, alf4, bta4, gam4) then begin
oflag := 2;
end;
HV_Move;
end;
end;
if xflag and 4 = 4 then begin
for i := 1 to 3 do
for k := 1 to 3 do begin
arr3[i, k] := arr2[i, k] * lambda3; // arr3 = arr2 * λ3
end;
difference2(arr1, arr3, arr4); // arr4 = arr1 - arr3 λ3
det := difference3(arr4, a, h, b, g, f, c);
if abs(det) < 1E-12 then begin
// 因数分解
if factorization(a, h, b, g, f, c, alf5, bta5, gam5, alf6, bta6, gam6) then begin
oflag := 4;
end;
HV_Move;
end;
end;
}
if dflag <> 0 then timer1.Interval := 50;
//-----------------------------------------------------------------------------------------
iflag := false;
// 因数分解ができた場合 因数分解が出来ても 答えが出ない場合もあります
// 因数分解値の一次式同士の連立方程式を解いても答えは出せますが、組み合わせが
// が発生するので、一次式と楕円の二元二次式の連立方程式を解きます
if (oflag and 1 = 1) and (dflag = 0) then begin
xflag := quadratic(A1, B1, C1, D1, E1, F1, alf1, bta1, gam1, x1, x2);
if xflag <> 0 then begin
y1 := - gam1 / bta1 - alf1 / bta1 * x1;
y2 := - gam1 / bta1 - alf1 / bta1 * x2;
dflag := 3;
iflag := True;
end;
xflag := quadratic(A1, B1, C1, D1, E1, F1, alf2, bta2, gam2, x3, x4);
if xflag <> 0 then begin
y3 := - gam2 / bta2 - alf2 / bta2 * x3;
y4 := - gam2 / bta2 - alf2 / bta2 * x4;
dflag := dflag or 12;
iflag := True;
end;
end;
// 最初の実数解のみ使用
{
if (oflag and 2 = 2) and (dflag < 15) then begin
xflag := quadratic(A2, B2, C2, D2, E2, F2, alf3, bta3, gam3, x1, x2);
if xflag <> 0 then begin
y1 := - gam3 / bta3 - alf3 / bta3 * x1;
y2 := - gam3 / bta3 - alf3 / bta3 * x2;
dflag := 3;
iflag := True;
end;
xflag := quadratic(A2, B2, C2, D2, E2, F2, alf4, bta4, gam4, x3, x4);
if xflag <> 0 then begin
y3 := - gam4 / bta4 - alf4 / bta4 * x3;
y4 := - gam4 / bta4 - alf4 / bta4 * x4;
dflag := dflag or 12;
iflag := True;
end;
end;
if (oflag and 4 = 4) and (dflag < 15) then begin
xflag := quadratic(A1, B1, C1, D1, E1, F1, alf5, bta5, gam5, x1, x2);
if xflag <> 0 then begin
y1 := - gam5 / bta5 - alf5 / bta5 * x1;
y2 := - gam5 / bta5 - alf5 / bta5 * x2;
dflag := 3;
iflag := True;
end;
xflag := quadratic(A1, B1, C1, D1, E1, F1, alf6, bta6, gam6, x3, x4);
if xflag <> 0 then begin
y3 := - gam6 / bta6 - alf6 / bta6 * x3;
y4 := - gam6 / bta6 - alf6 / bta6 * x4;
dflag := dflag or 12;
iflag := True;
end;
end;
}
//------------------------------------------------------------------------------------
// 軸角度を30°にしなかった場合に必要になる計算
// 因数分解できない場合と、因数分解が出来ても、β値(yの項)がゼロになる場合の計算です。
//------------------------------------------------------------------------------------
if (dflag = 0) and checkbox1.Checked then begin
// 軸角ゼロで水平移動
if (a <> 0) and (abs(h) < 1E-20) and (abs(b) < 1E-20) and (g <> 0) and (abs(f) < 1E-8) and (c <> 0) then begin
// 因数分解
if factorization(a, h, b, g, f, c, alf1, bta1, gam1, alf2, bta2, gam2) then begin
oflag := 1;
end;
if oflag <> 0 then begin
x1 := - gam1 / alf1;
x2 := - gam2 / alf2;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, x1, x2, true, y1, y2, y3, y4);
if dflag = 1 then begin
x2 := x1;
dflag := 3;
end
else begin
if dflag = 2 then begin
x1 := x2;
y1 := y3;
y2 := y4;
dflag := 3;
end
else begin
if dflag = 3 then begin
x3 := x2;
x4 := x2;
x2 := x1;
dflag := 15;
end;
end;
end;
iflag := true;
end;
end;
// 軸角ゼロで垂直移動
if (abs(a) < 1E-20) and (abs(h) < 1E-20) and (b <> 0) and (abs(g) < 1E-8) and (f <> 0) and (c <> 0) then begin
// 因数分解
if factorization(b, h, a, f, g, c, alf1, bta1, gam1, alf2, bta2, gam2) then begin
oflag := 1;
end;
if oflag <> 0 then begin
y1 := - gam1 / alf1;
y2 := - gam2 / alf2;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, y1, y2, false, x1, x2, x3, x4);
if dflag = 4 then begin
y2 := y1;
dflag := 3;
end;
if dflag = 8 then begin
y1 := y2;
x1 := x3;
x2 := x4;
dflag := 3;
end;
if dflag = 12 then begin
y3 := y2;
y4 := y2;
y2 := y1;
dflag := 15;
end;
iflag := true;
end;
end;
// 軸角ゼロで楕円同軸 ar > br
if (abs(a) < 1E-11) and (abs(h) < 1E-20) and (b <> 0) and (abs(g) < 1E-8) and (abs(f) < 1E-20) and (c <> 0) then begin
y1 := sqrt(abs(c / b));
y2 := - y1;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, y1, y2, false, x1, x2, x3, x4);
if dflag = 4 then begin
y2 := y1;
x3 := x1;
x4 := x2;
dflag := 3;
end;
if dflag = 8 then begin
y1 := y2;
x1 := x3;
x2 := x4;
dflag := 3;
end;
if dflag = 12 then begin
y3 := y2;
y4 := y1;
dflag := 15;
end;
end;
// 軸角ゼロで同軸 br > ar
if (a <> 0) and (abs(h) < 1E-20) and (abs(b) < 1E-11) and (abs(g) < 1E-20) and (abs(f) < 1E-8) and (c <> 0) then begin
x1 := sqrt(abs(c / a));
x2 := - x1;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, x1, x2, true, y1, y2, y3, y4);
if dflag = 1 then begin
x2 := x1;
y3 := y1;
y4 := y2;
dflag := 3;
end
else begin
if dflag = 2 then begin
x1 := x2;
y1 := y3;
y2 := y4;
dflag := 3;
end
else begin
if dflag = 3 then begin
x3 := x2;
x4 := x1;
dflag := 15;
end;
end;
end;
end;
// 軸角ゼロで同軸 br 又は ar 近似
if (a <> 0) and (abs(h) < 1E-20) and (abs(b) < 1E-20) and (abs(g) < 1E-20) and (abs(f) < 1E-20) and (c <> 0) then begin
x1 := sqrt(abs(-c / a));
x2 := - x1;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, x1, x2, true, y1, y2, y3, y4);
if dflag = 1 then begin
x2 := x1;
y3 := y1;
y4 := y2;
dflag := 3;
end
else begin
if dflag = 2 then begin
x1 := x2;
y1 := y3;
y2 := y4;
dflag := 3;
end
else begin
if dflag = 3 then begin
x3 := x2;
x4 := x1;
dflag := 15;
end;
end;
end;
end;
// 楕円比が等しくて軸角0、水平方向移動
if (abs(a) < 1E-13) and (abs(h) < 1E-20) and (abs(b) < 1E-13) and (g <> 0) and (abs(f) < 1E-20) and (c <> 0) then begin
x1 := -c / g / 2;
x2 := x1;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, x1, x2, true, y1, y2, y3, y4);
if dflag = 3 then begin
dflag := 3;
end;
end;
// 楕円比が等しくて軸角0、垂直方向移動
if (abs(a) < 1E-13) and (abs(h) < 1E-20) and (abs(b) < 1E-13) and (abs(g) < 1E-20) and (f <> 0) and (c <> 0) then begin
y1 := -c / f / 2;
y2 := y1;
dflag := quadratic5(A1, B1, C1, D1, E1, F1, y1, y2, false, x1, x2, x3, x4);
if dflag = 12 then begin
dflag := 3;
end;
end;
end;
//-------------------------------------------------------------------------------------------------------------------
// 座標戻し 楕円の角度を元の角度に戻します
if dflag and 1 = 1 then xyconvert(x1, y1);
if dflag and 2 = 2 then xyconvert(x2, y2);
if dflag and 4 = 4 then xyconvert(x3, y3);
if dflag and 8 = 8 then xyconvert(x4, y4);
for i := 0 to 3 do begin
xx[i] := 0;
yy[i] := 0;
xy[i] := 0;
end;
// 接点二個のチェック 同一点座標の確認
if dflag and 1 = 1 then xx[0] := round(x1 * 1000) / 1000;
if dflag and 2 = 2 then xx[1] := round(x2 * 1000) / 1000;
if dflag and 4 = 4 then xx[2] := round(x3 * 1000) / 1000;
if dflag and 8 = 8 then xx[3] := round(x4 * 1000) / 1000;
if dflag and 1 = 1 then yy[0] := round(y1 * 1000) / 1000;
if dflag and 2 = 2 then yy[1] := round(y2 * 1000) / 1000;
if dflag and 4 = 4 then yy[2] := round(y3 * 1000) / 1000;
if dflag and 8 = 8 then yy[3] := round(y4 * 1000) / 1000;
if (dflag = 15) then begin
dflag := 0;
for i := 0 to 3 do xy[i] := 0;
for i := 0 to 3 do
for k := i to 3 do
if (k <> i) and (xx[i] = xx[k]) and (yy[i] = yy[k]) then inc(xy[k]);
for i := 0 to 3 do if xy[i] = 0 then dflag := dflag + round(power(2, i));
end;
if dflag = 3 then
if (xx[0] = xx[1]) and (yy[0] = yy[1]) then dflag := 1;
if dflag = 12 then
if (xx[2] = xx[3]) and (yy[2] = yy[3]) then dflag := 4;
if iflag then image1.Canvas.TextOut(image1.Width - 20, 0, '因')
else if dflag <> 0 then image1.Canvas.TextOut(image1.Width - 20, 0, '〇');
if (dflag = 1) or (dflag = 4) or (dflag = 13) or (dflag = 14) then timer1.Interval := 1000
else
if iflag or (dflag = 0) then timer1.Interval := 50;
if dflag = 0 then timerF := false;
//-----------------------------------------------------------------------------------------
i := 1;
// 楕円弧上にある交点のみ表示
if dflag and 1 = 1 then begin
// 円弧上にあるかどうか判定 円弧上ならTrue
if intersection_judge(Ellipse1, Ellipse2, x1, y1) then begin
// 交点丸表示
EllipseDraw(x1, y1);
// 座標値表示
TextoutXY(x1, y1, i, i);
inc(i);
end;
end;
if dflag and 2 = 2 then begin
if intersection_judge(Ellipse1, Ellipse2, x2, y2) then begin
EllipseDraw(x2, y2);
TextoutXY(x2, y2, i, i);
inc(i);
end;
end;
if dflag and 4 = 4 then begin
if intersection_judge(Ellipse1, Ellipse2, x3, y3) then begin
EllipseDraw(x3, y3);
TextoutXY(x3, y3, i, i);
inc(i);
end;
end;
if dflag and 8 = 8 then begin
if intersection_judge(Ellipse1, Ellipse2, x4, y4) then begin
EllipseDraw(x4, y4);
TextoutXY(x4, y4, i, i);
end;
end;
end;
// 角度の範囲0から360の範囲に調整
function TForm1.angle_amendment(angle : Extended): Extended;
begin
repeat
if angle >= 360 then angle := angle - 360;
if angle < 0 then angle := angle + 360;
until (angle < 360) and (angle >= 0);
Result := angle;
end;
// 角度の範囲0から180の範囲に調整
function TForm1.angle180_amendment(angle : Extended): Extended;
begin
repeat
if angle >= 180 then angle := angle - 180;
if angle < 0 then angle := angle + 180;
until (angle < 180) and (angle >= 0);
Result := angle;
end;
//------------------------------------------------
// 楕円弧上に交点があるかどうかの判定を行います
// Ellipse1 Ellipse2 楕円
// X 交点座標 X
// Y 交点座標 Y
//------------------------------------------------
function TForm1.intersection_judge(Ellipse1, Ellipse2: TEllipse; X, Y: Extended): boolean;
var
qxy : Extended;
endang : Extended;
begin
Result := False;
x := (x + xshift) / scale;
y := (y + yshift) / scale;
// 楕円弧1に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse1.fcy),(x - Ellipse1.fCx)) / pi * 180 - Ellipse1.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse1.endAngle;
if Ellipse1.startAngle > Ellipse1.endAngle then begin
endang := Ellipse1.endAngle + 360;
if qxy < Ellipse1.startAngle then qxy := qxy + 360;
end;
// 楕円弧1の弧上に交点があるか判定
if (qxy >= Ellipse1.startAngle) and (qxy <= endang) or
(Ellipse1.startAngle = Ellipse1.endAngle) then else exit;
// 楕円弧2に対する交点の位置の角度計算
qxy := arctan2((y - Ellipse2.fcy),(x - Ellipse2.fCx)) / pi * 180 - Ellipse2.fAngle;
qxy := angle_amendment(qxy);
endang := Ellipse2.endAngle;
if Ellipse2.startAngle > Ellipse2.endAngle then begin
endang := Ellipse2.endAngle + 360;
if qxy < Ellipse2.startAngle then qxy := qxy + 360;
end;
// 楕円弧2の弧上に交点があるか判定
if (qxy >= Ellipse2.startAngle) and (qxy < endang) or
(Ellipse2.startAngle = Ellipse2.endAngle) then Result := True
else Result := False;
end;
var
inpchF : boolean;
//--------------------------------------------------------
// 入力された楕円の描画
// 楕円作図のy方向は、楕円作図ルーチンで修正されます。
//--------------------------------------------------------
procedure TForm1.inputdata_drawing;
const
K = 100;
km = 1 / K;
var
left_min, left_max : Extended;
top_min, top_max : Extended;
all_width, all_height: Extended;
ac1, ac2, acl : Extended;
q1, q2 : integer;
x1, x2, y1, y2 : Extended;
dx1, dy1, dq1 : Extended;
dx2, dy2, dq2 : Extended;
begin
inpchF := true;
// 座標軸を30°にしなかった場合 楕円の角度の0.01°以下丸めを行います。
// 座標軸30°の時は、殆どが因数分解可能ですが、座標軸軸ゼロの時
// 因数分解出来ない条件が沢山発生します。
// 座標軸がゼロの時、軸角がゼロで因数分解不可か軸角がゼロでなく因数分解可能かの
// 判定に角度0.01°程度が必要となます。
// 軸角が0°以上で0.01°以下の時、計算されない領域が発生することになります。
// 座標軸ゼロの時はその領域での計算を避ける様にします。
// 基本的には座標軸は30°でなくても、0.01°以上あれば良いことになります。
if checkbox1.Checked then begin
q1 := Trunc(abs(Ellipse1.fAngle) / 90);
q2 := Trunc(abs(Ellipse2.fAngle) / 90);
ac1 := abs(Ellipse1.fAngle) - q1 * 90;
ac2 := abs(Ellipse2.fAngle) - q2 * 90;
if (ac1 < km) and (ac2 < km) then begin
Ellipse1.fAngle := Ellipse1.fAngle * k;
q1 := round(Ellipse1.fAngle);
Ellipse1.fAngle := q1 / k;
// angle_q1_edit.Text := floatTostr(Ellipse1.fAngle);
Ellipse2.fAngle := Ellipse2.fAngle * k;
q2 := round(Ellipse2.fAngle);
Ellipse2.fAngle := q2 / k;
// angle_q2_edit.Text := floatTostr(Ellipse2.fAngle);
end;
end;
// 表示設定用半径の大きい方の選択
ac1 := Ellipse1.fRad_X;
if Ellipse1.fRad_X < Ellipse1.fRad_Y then begin
ac1 := Ellipse1.fRad_Y;
end;
ac2 := Ellipse2.fRad_X;
if Ellipse2.fRad_X < Ellipse2.fRad_Y then begin
ac2 := Ellipse2.fRad_Y;
end;
// 計算スケール変換
acl := ac1;
if acl < ac2 then acl := ac2;
scale := 200 / acl;
ac1 := ac1 * scale;
ac2 := ac2 * scale;
ar1 := Ellipse1.fRad_X * scale;
br1 := Ellipse1.fRad_Y * scale;
ar2 := Ellipse2.fRad_X * scale;
br2 := Ellipse2.fRad_Y * scale;
xo1 := Ellipse1.fCx * scale;
xo2 := Ellipse2.fCx * scale;
yo1 := Ellipse1.fcy * scale;
yo2 := Ellipse2.fcy * scale;
dq2 := Ellipse1.fAngle - Ellipse2.fAngle;
repeat
if dq2 >= 180 then dq2 := dq2 - 180;
if dq2 < 0 then dq2 := dq2 + 180;
until (dq2 < 180) and (dq2 >= 0);
dq1 := 180 - dq2;
// 楕円の値の確認二つの楕円の値が近い場合計算しないフラグセット
if (abs(dq2) < 1E-3) or (abs(dq1) < 1E-3) then begin
if (abs(xo1 - xo2) < 1E-7) and
(abs(yo1 - yo2) < 1E-7) and
(abs(ar1 - ar2) < 1E-7) and
(abs(br1 - br2) < 1E-7) then begin
application.MessageBox('楕円の値が殆ど同じです','楕円の値',0);
inpchF := false;
end;
end;
if (abs(dq2 - 90) < 1E-3) then begin
if (abs(xo1 - xo2) < 1E-7) and
(abs(yo1 - yo2) < 1E-7) and
(abs(ar1 - br2) < 1E-7) and
(abs(br1 - ar2) < 1E-7) then begin
application.MessageBox('楕円の値が殆ど同じです','楕円の値',0);
inpchF := false;
end;
end;
// 座標変換 楕円1を原点へ移動
xshift := xo1;
xo2 := xo2 - xshift;
xo1 := 0;
yshift := yo1;
yo2 := yo2 - yshift;
yo1 := 0;
// 画像表示範囲設定
left_min := xo1 - ac1;
if xo2 - ac2 < left_min then left_min := xo2 - ac2;
left_max := xo1 + ac1;
if xo2 + ac2 > left_max then left_max := xo2 + ac2;
all_width := left_max - left_min; // 最大幅
top_min := yo1 - ac1;
if yo2 - ac2 < top_min then top_min := yo2 - ac2;
top_max := yo1 + ac1;
if yo2 + ac2 > top_max then top_max := yo2 + ac2;
all_height := top_max - top_min; // 最大高さ
// 変倍率の設定
top_max := (image1.Height - draw_margin * 2) / all_Height;
magnification := (image1.Width - draw_margin * 2) / all_width;
if magnification > top_max then magnification := top_max;
// 移動量の設定
shift_x := left_min * magnification;
shift_y := top_min * magnification;
// イメージクリア
imageClear;
image1.Canvas.Brush.Style := bsClear;
// 楕円1作図
x1 := xo1 * magnification - shift_x + draw_margin;
y1 := yo1 * magnification - shift_y + draw_margin;
x2 := xo2 * magnification - shift_x + draw_margin;
y2 := yo2 * magnification - shift_y + draw_margin;
EllipseEx(image1.Canvas,
image1.Height, // canvas高さ
3, // 線種
1, // 線幅
clRed, // 色
ar1 * magnification, // 半径a
br1 * magnification, // 半径b
x1, // 中心位置x
y1, // 中心位置y
Ellipse1.fAngle, // 回転角 deg
Ellipse1.startAngle, // 作図開始角
Ellipse1.endAngle); // 作図終了角
EllipseEx(image1.Canvas,
image1.Height, 0, 1, clRed, ar1 * magnification,
br1 * magnification, x1, y1, Ellipse1.fAngle,
Ellipse1.endAngle, Ellipse1.startAngle);
// 楕円2作図
EllipseEx(image1.Canvas,
image1.Height, 3, 1, clBlue, ar2 * magnification,
br2 * magnification, x2, y2, Ellipse2.fAngle,
Ellipse2.startAngle, Ellipse2.endAngle);
EllipseEx(image1.Canvas,
image1.Height, 0, 1, clBlue, ar2 * magnification,
br2 * magnification, x2, y2, Ellipse2.fAngle,
Ellipse2.endAngle, Ellipse2.startAngle);
// 中心線作図
dq1 := Ellipse1.fAngle / 180 * pi;
dx1 := cos(dq1) * 30;
dy1 := sin(dq1) * 30;
dq2 := (90 + Ellipse1.fAngle) / 180 * pi;
dx2 := cos(dq2) * 30;
dy2 := sin(dq2) * 30;
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed,
x1 - dx1, y1 - dy1, x1 + dx1, y1 + dy1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clRed,
x1 - dx2, y1 - dy2, x1 + dx2, y1 + dy2, true);
dq1 := Ellipse2.fAngle / 180 * pi;
dx1 := cos(dq1) * 30;
dy1 := sin(dq1) * 30;
dq2 := (90 + Ellipse2.fAngle) / 180 * pi;
dx2 := cos(dq2) * 30;
dy2 := sin(dq2) * 30;
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue,
x2 - dx1, y2 - dy1, x2 + dx1, y2 + dy1, true);
StraightLineDraw(image1.Canvas, image1.Height, 1, 1, clBlue,
x2 - dx2, y2 - dy2, x2 + dx2, y2 + dy2, true);
end;
var
inpf : boolean;
// 計算データー入力処理 計算開始
procedure TForm1.SelectBtnClick(Sender: TObject);
var
ch: integer;
begin
timer1.Enabled := False;
// 楕円1のデーター
val(radius_a1_Edit.Text, Ellipse1.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の半径a1数値ではありません', '楕円1の半径a1', 0);
exit;
end;
if Ellipse1.fRad_X <= 0 then begin
application.MessageBox('楕円1の半径a1が0又は0以下です', '楕円1の半径a1', 0);
exit;
end;
val(radius_b1_Edit.Text, Ellipse1.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の半径b1数値ではありません', '楕円1の半径b1', 0);
exit;
end;
if Ellipse1.fRad_Y <= 0 then begin
application.MessageBox('楕円1の半径b1が0又は0以下です', '楕円1の半径b1', 0);
exit;
end;
val(Center_x1_Edit.Text, Ellipse1.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の中心位置x1数値ではありません', '楕円1の中心位置x1', 0);
exit;
end;
val(Center_y1_Edit.Text, Ellipse1.fcy, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の中心位置y1数値ではありません', '楕円1の中心位置y1', 0);
exit;
end;
val(angle_q1_Edit.Text, Ellipse1.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の角度θ1数値ではありません', '楕円1の角度θ1', 0);
exit;
end;
val(Start_angle_S1.Text, Ellipse1.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の開始角数値ではありません', '楕円1の開始角S1', 0);
exit;
end;
val(End_angle_E1.Text, Ellipse1.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円1の終了角数値ではありません', '楕円1の終了角E1', 0);
exit;
end;
// 楕円2のデーター
val(radius_a2_Edit.Text, Ellipse2.fRad_X, ch);
if ch <> 0 then begin
application.MessageBox('楕円2半径a2数値ではありません', '楕円2の半径a2', 0);
exit;
end;
if Ellipse2.fRad_X <= 0 then begin
application.MessageBox('楕円2の半径a2が0又は0以下です', '楕円2の半径a2', 0);
exit;
end;
val(radius_b2_Edit.Text, Ellipse2.fRad_Y, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の半径b2数値ではありません', '楕円2の半径b2', 0);
exit;
end;
if Ellipse2.fRad_Y <= 0 then begin
application.MessageBox('楕円2の半径b2が0又は0以下です', '楕円2の半径b2', 0);
exit;
end;
val(Center_x2_Edit.Text, Ellipse2.fCx, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の中心位置x2数値ではありません', '楕円2の中心位置x2', 0);
exit;
end;
val(Center_y2_Edit.Text, Ellipse2.fcy, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の中心位置y2数値ではありません', '楕円2の中心位置y2', 0);
exit;
end;
val(angle_q2_Edit.Text, Ellipse2.fAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の角度θ2数値ではありません', '楕円2の角度θ2', 0);
exit;
end;
val(Start_angle_S2.Text, Ellipse2.startAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の開始角数値ではありません', '楕円2の開始角S2', 0);
exit;
end;
val(End_angle_E2.Text, Ellipse2.endAngle, ch);
if ch <> 0 then begin
application.MessageBox('楕円2の終了角数値ではありません', '楕円2の終了角E2', 0);
exit;
end;
// 入力された楕円角度の値修正 0 ~ 360 の範囲に入る様にします。
Ellipse1.fAngle := angle_amendment(Ellipse1.fAngle);
Ellipse2.fAngle := angle_amendment(Ellipse2.fAngle);
Ellipse1.startAngle := angle_amendment(Ellipse1.startAngle);
Ellipse1.endAngle := angle_amendment(Ellipse1.endAngle);
Ellipse2.startAngle := angle_amendment(Ellipse2.startAngle);
Ellipse2.endAngle := angle_amendment(Ellipse2.endAngle);
inputdata_drawing; // 入力画像表示
if inpchF then // 入力値に問題が無かったら交点計算
cross_calc; // 交点計算
if inpF then timer1.Enabled := true;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
if timer1.Enabled then begin
timer1.Enabled := false;
inpF := False;
timerf := false;
end
else begin
timer1.Enabled := True;
timerf := true;
inpF := true;
end;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if timerf then begin
Ellipse1.fAngle := Ellipse1.fAngle + 0.125;
Ellipse2.fAngle := Ellipse2.fAngle + 0.25;
angle_q2_Edit.Text := floatTostr(Ellipse2.fAngle);
angle_q1_Edit.Text := floatTostr(Ellipse1.fAngle);
SelectBtnClick(nil);
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
clientHeight := 560;
clientWidth := 1000;
top := (screen.Height- height) div 2;
left := (screen.Width - width) div 2;
// 線種配列确保
setlength(LPitch, LineN);
// 線種データーセット
LPitch[0].segment := 2; // 破線
LPitch[0].Pitch[0] := 6;
LPitch[0].Pitch[1] := 3;
LPitch[1].segment := 4; // 1点鎖線
LPitch[1].Pitch[0] := 15;
LPitch[1].Pitch[1] := 3;
LPitch[1].Pitch[2] := 3;
LPitch[1].Pitch[3] := 3;
LPitch[2].segment := 6; // 2点鎖線
LPitch[2].Pitch[0] := 18;
LPitch[2].Pitch[1] := 3;
LPitch[2].Pitch[2] := 3;
LPitch[2].Pitch[3] := 3;
LPitch[2].Pitch[4] := 3;
LPitch[2].Pitch[5] := 3;
// イメージクリア
imageClear;
image1.Canvas.Font.Name := 'MS ゴシック';
// image1.Canvas.Font.Style := [fsbold];
image1.Canvas.Font.Height := 14;
end;
end.
此処でダウンロードしたzipファイルの中の Ellipse_factorization_X_New フォルダー側が多倍長演算のプログラムです。
![]() Ellipsefactorization.zip
Ellipsefactorization.zip